SİHİRLİ KARELER VE MOORE- PENROSE GENELLEŞTİRİLMİŞ İNVERSİ
ORTA ÖĞRETİMDE LİMİT KAVRAMININ OLUŞTURULMASINA YÖNELİK BİR ÇALIŞMA
3 Kasım 2018Simetri Öğretimi
3 Kasım 2018| Başlığı : | SİHİRLİ KARELER VE MOORE- PENROSE GENELLEŞTİRİLMİŞ İNVERSİ |
| Konu : | Bu çalışmada nxn biçimindeki reel girişlere sahip sihirli kareleri (matrisleri) inceleyeceğiz. |
| Yazar : | Prof.Dr. Fikri Akdeniz |
| Tarih : | 09.04.2003 |
| E-mail : |
Özet: Bu çalışmada nxn biçimindeki reel girişlere sahip sihirli kareleri (matrisleri) inceleyeceğiz. Bu matrislerde tüm satır ve sütunların toplamları aynı s sabit sayısına eşittir. Ayrıca bazı singüler (tekil) sihirli matrislerin Moore-Penrose inverslerini vereceğiz.
Anahtar sözcükler: Alfabetik sihirli kare, Moore-Penrose inversi, sihirli kare, sihirli sabit
1. Giriş
Tanım.1. ![]() sayılarının
sayılarının ![]() kare içine her satır, sütun ve köşegen toplamları aynı s sayısına eşit olacak şekildeki düzenlenmesine -inci mertebeden sihirli- kare denir. ns= 1+2+…+n2 olduğundan s=n(n2+1)/2 bulunur. s sayısına “sihirli sabit” denir. Yalnız satır ve sütun toplamlarının tümü sabit bir sayıya eşit olan kare matrise yarı- sihirli (semi-magic) kare denir.
kare içine her satır, sütun ve köşegen toplamları aynı s sayısına eşit olacak şekildeki düzenlenmesine -inci mertebeden sihirli- kare denir. ns= 1+2+…+n2 olduğundan s=n(n2+1)/2 bulunur. s sayısına “sihirli sabit” denir. Yalnız satır ve sütun toplamlarının tümü sabit bir sayıya eşit olan kare matrise yarı- sihirli (semi-magic) kare denir.
3 ![]() 3 tipindeki aşağıdaki sihirli karelerde 1 den 9 a kadar sayılarla oluşturulan aşağıdaki sihirli karede sihirli sabit 3( 32 +1)/2 =15 tir.
3 tipindeki aşağıdaki sihirli karelerde 1 den 9 a kadar sayılarla oluşturulan aşağıdaki sihirli karede sihirli sabit 3( 32 +1)/2 =15 tir.
M= 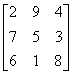
Normal sihirli kare her bir sayıyı sırayla n2+1 den çıkararak diğer bir sihirli kareye dönüştürülebilir. Örneğin, yukarıdaki M sihirli karede n2+1 =10 olduğundan her bir sayıyı 10 dan çıkararak
| 8 | 1 | 6 |
| 3 | 5 | 7 |
| 4 | 9 | 2 |
yeni sihirli kare elde edilir. Bu karelere kendine benzer sihirli kare denir.
Şimdi Albert Dürer (1471-1528) tarafından yapılan “Melancolia” tablosunda yer alan ve annesinin ölüm tarihi 1514 yılını da içeren sihirli kareyi inceleyelim.
|
16 |
03 |
02 |
13 |
|
05 |
10 |
11 |
08 |
|
09 |
06 |
07 |
12 |
|
04 |
15 |
14 |
01 |
Her yönde satır ve sütun toplamları , köşegen toplamları 34 tür. Ayrıca toplamları 34 ü veren çok sayıda kalıp vardır:
16+3+5+10=34, 16+4+1+13=34, 5+9+12+8=34, 3+9+14+ 8 =34, 2+5+15+12=34, 3+9+15+7=34, 3+5+15+11=34, 5+4+14+11=34 , 16+9+7+2 =34, 3+6+12+13=34, 10+15+1+8=34
Sihirli kareler tarihsel süreç içinde Araplar, Çin, Antik Yunan, Hindistan ve Japonya’da düzenlenmişti . Çin’deki bir rivayete göre, M.Ö. 2000 li yıllarda büyük Çin imparatoru Yu , bir zamanlar sarı nehir kıyısında hazır bekleyerek kaplumbağalar sarı nehirde sudan dışarı çıktıklarında sırtlarındaki
|
4 |
9 |
2 |
|
3 |
5 |
7 |
|
8 |
1 |
6 |
biçimindeki LO-SHU denilen sihirli kareyi izlemekten keyif alıyordu. Avrupa’nın sihirli karelerle tanışması 15. asırda İstanbul’da yaşamış olan Yunanlı matematikçi Emanual Moschopulos ile gerçekleşmiştir (Ball ve Coxeter (1987)). Sihirli kareler matematik tarihi içinde pek çok araştırmacının ilgisini çekti. Bunların arasında Yung Hui, Moschopoulos, Stifel, Pascal, Euler ve 19 . yüzyılda Bieberbach, Vebler ve D.M. Lehmer’i sayabiliriz. Ayrıca Loyd, Dudeney ve büyük Martin Gardner gibi bulmaca çözerlerin çalışmalarını da eklemek gerekir.
2. Benjamin Franklin’in sihirli kareleri
Matematik dünyasında bir çoğu hala bilinmeyen bazı sihirli kareler 18. yüzyılda yaşamış olan Benjamin Franklin (1706-1790) tarafından oluşturulmuştur. Daha önce hiç yayınlanmamış olanı (Şekil 1) Pasles (2001) de incelenmiştir. Bir yazar, diplomat ve bilim adamı (fizikçi ve matematikçi ) olarak Franklin kendi yaşadığı dönemde ve günümüzde övgüye değer biridir. Örneğin, Londra ve Paris Bilimler Akademilerinin bilimsel üyeliğe seçtiği tek Amerikandı ve uzun yıllar da tek kalmıştı. Franklin’in matematiksel yaşamı karelerin kendileri ve almanaklardır. Franklin’in formal eğitimi iki yıldan daha kısa bir sürede son bulmuştur. Esas itibariyle kendi kendini yetiştirmiştir. Franklin Şekil 1 de verdiği kareleri nasıl yazmıştı? El yazması dışında karşılaştırmak için elimizde bir belge de yoktur. Günümüze kadar bir çok araştırmacı Franklin karelerini incelediler. Bunların en ilginci lineer cebir kavramlarını kullanarak Şekil 1 in incelenmesidir (Henrich (1991)).
|
52 |
61 |
04 |
13 |
20 |
29 |
36 |
45 |
|
14 |
03 |
62 |
51 |
46 |
35 |
30 |
19 |
|
53 |
60 |
05 |
12 |
21 |
28 |
37 |
44 |
|
11 |
06 |
59 |
54 |
43 |
38 |
27 |
22 |
|
55 |
58 |
07 |
10 |
23 |
26 |
39 |
42 |
|
09 |
08 |
57 |
56 |
41 |
40 |
25 |
24 |
|
50 |
63 |
02 |
15 |
18 |
31 |
34 |
47 |
|
16 |
01 |
64 |
49 |
48 |
33 |
32 |
17 |
Şekil 1 Franklin’in 8×8 yarı-sihirli
Şekil 1 de satırların ve sütunların toplamı 260 dır. Yarı-sihirli karedir. Köşegen toplamları 260 değildir. Görüldüğü gibi k ve 65-k sayıları aynı satırda yer almaktadır.( I. satırda k=4 , 65-k=61; k=52 65-k=13; k=20 65-k=45; k=29 65-k= 36 ) ; köşelerdeki 2×2 karelerin sayılar toplamı=130 ; 2×4 veya 4×2 dikdörtgenlerdeki sayılar toplamı =260 dir.
Dört köşedeki 2×2 sayılar toplamı= 130 dur.( I. köşede 52+61+14+3=130 v.s). Her bir satırın ve sütunun toplamının yarısı da 130 dır.
3. Alfabetik sihirli kareler
Hristiyan ve islam geleneğinde yatay ve dikey yönde, ayrıca köşegenlerin her ikisine göre de simetrik yapıda sözcüklerin oluşturduğu alfabetik sihirli kareler olduğu bilinmektedir. Bunların kökeni M.Ö. 1. Asır ve M.S. 6. Asıra kadar dayanmaktadır. (Aldo Domenicano ve Hargittai (2000)).İtalya’daki küçük Capestrano kasabasının güney doğusunda 40 km kadar uzaklıkta 8. Asırda inşa edilmiş ve yeniden onarıldıktan sonra şu andaki haliyle 12. Yüzyıldan kalma çok iyi korunmuş olan San Pietro ad Oratorium kilisesinin girişinde 5×5 biçiminde blok kireç taşı üzerinde oyulmuş beş sözcükten oluşan alfabetik sihirli kare vardır. AREPO dışında dördü Latince’den gelen bu sözcükler:
ROTAS , OPERA, TENET , AREPO, SATOR
dır. TENET her iki yönden okunduğunda değişmeyen sözcüktür.
|
R |
O |
T |
A |
S |
|
O |
P |
E |
R |
A |
|
T |
E |
N |
E |
T |
|
A |
R |
E |
P |
O |
|
S |
A |
T |
O |
R |
4. Yarı-sihirli kareler ve Moore-Penrose (MP) inversi
Booth ve Booth (1955) de ifade edildiği gibi singüler olmayan bir sihirli karenin elemanlarıyla oluşturulan bir matrisin tersi de bir sihirli karedir. s “sihirli-sabit” olmak üzere bir matrisin tersinin satır ve sütunlarının toplamları 1/s ye eşittir. Aşağıdaki 3×3 sihirli kareyi ele alalım. Singüler olmayan M matrisi için
M= ![]() =
= 
Det(M)= ![]() -360 tır.
-360 tır.
M-1= 

Görülebileceği gibi M-1 matrisinin satır ve sütun toplamları 1/15 tir. Aynı özellik köşegen toplamları için de geçerlidir. Dürer’in sihirli karesine bakıldığında karşılık gelen kare matris singüler (tekil) ve rankı 3 tür. Bu nedenle Booth ve Booth (1955) deki sonuç uygulanamaz. O halde matrislerin Moore-Penrose (MP) inverslerinin de sihirli kare özelliklerini taşıyıp taşımadığını öğrenmek istiyoruz.
Bir A matrisinin A+ ile gösterilen MP inversi aşağıdaki dört koşulu sağlarsa A+ tek olarak tanımlanır.
(i) AA+A=A
(ii) A+AA+=A+
(iii) (AA+)¢=(AA+)
(iv) (A+A)¢=A+A
A bir kare matris olmasa bile bu invers daima vardır (Rao ve Mitra (1971)). Yalnız (i) koşulu sağlanırsa , yani AA-A=A ise, A- ye A nın g-inversi denir. Her matris g-inverse sahiptir, fakat tek olmayabilir.
Şimdi Dürer tarafından yapılan “Melancolia” resminde yer alan aşağıdaki meşhur sihirli kareyi düşünelim:
D= 
Satır, sütun ve köşegen toplamları 34, dört köşedeki 2×2 alt kare matrislerin elemanlarının toplamı da 34 tür. D singüler bir matristir ve rankı 3 tür. D , 4×4 tipinde sihirli kare matrisin MP-inversi de sihirli kare olan bir matrise örnektir. Görüldüğü gibi D nin MP-inversi:
D+= ![]()

dir. MP-inversin (i)-(iv) koşulları sağlanır (Trenkler (1994)). D matrisini
 D=
D= 
biçiminde parçalara ayırdığımızda
D11=  , det(D) =136
, det(D) =136 ![]() , ve rank(D11) =3 tür. D12=
, ve rank(D11) =3 tür. D12= ![]() ‘, D21=
‘, D21= ![]() , D22= 1 ve
, D22= 1 ve ![]() olmak üzere
olmak üzere
D+= 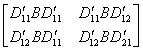
bulunur. Görülebileceği gibi satır, sütun ve köşegen toplamları , dört köşedeki alt kare matrislerdeki sayılar toplamı da 1/34 tür. O halde aşağıdaki teoremi verebiliriz.
TEOREM. Bir A kare matrisinin yarı-sihirli olabilmesi için gerek ve yeter koşul Aj=A¢j=sj dir. Burada j¢=(1,1,…,1) nx1 tipinde vektördür.
Benjamin Franklin tarafından oluşturulan Şekil 1 deki 8×8 kare matrisi A olsun. A nın öz değerlerini inceleyelim: Öz değerlerin üçü
![]() ,
, ![]()
![]()
ve diğerleri sıfır olmaktadır. Trace(A)=228= ![]() dır. rank (A)=3 tür. Görüldüğü gibi Aj=A¢j=sj dir.
dır. rank (A)=3 tür. Görüldüğü gibi Aj=A¢j=sj dir.
Kaynaklar
Ball, W.W.R. and Coxeter, H.S.M.(1987). Mathematical Recreations and Essays. 13th Edition. Dover, NewYork, and University of Toronto Press.Booth, A. D. and Booth, K.H.V. (1955).
On magic squares. The Mathematical Gazette, 39, 132-133.Domenicano, A. and Hargittai, I. (2000).
Alphabetic magic square in a medieval church. The Mathematical Intelligencer, 22 (1), 52-53.Henrich, C. J. (1991).
Magic squares and linear algebra. Amer. Math. Monthly 98, 481-488.Pasles, P.C. (2001).
The lost squares of Dr. Franklin: Ben Franklin’s missing squares and the secret of the magic circle. TheAmerican Mathematical Monthly, 108, 489-511.Rao, C. R. And Mitra, S. K. (1971).
Generalized Inverse of Matrices and Its Applications, New York: John Wiley.Trenkler, G. (1994).
Singular magic squres. International Journal of Mathematical Education in Science and Technology, 25, 595-597.


